By David Hinds, Chuong Do, and Shirley Wu
In January we wrote about the challenging search for genetic influences on human longevity, touching on two of the most recent studies as examples of how elusive solid findings have been. Because one of these studies was a new version of a paper that was previously retracted, we took a particular interest to see if the concerns raised by the previous analysis were addressed. What follows is a technical review of “Genetic Signatures of Extreme Longevity in Humans”, published last month in PLoS ONE.
Although Paola Sebastiani and Thomas Perls (the main authors on both papers) do not directly discuss their previous study, their new version does appear to resolve many of the issues from the prior manuscript, and their GWAS results are substantially improved. They now report just one SNP clearly associated with longevity, rs2075650 near APOE. They also present a revised genetic model for predicting longevity based on 281 SNPs representing the common genetic variants most significantly associated with longevity in an analysis of 801 centenarians and 914 healthy control individuals.
As described in the paper, the performance of the model remains quite impressive:
- 89% sensitivity and 89% specificity (“area under the curve”=AUC=0.95) on the discovery set,
- 60% sensitivity and 58% specificity (AUC=0.58) on a replication set of 253 independent cases and 341 genetically-matched controls, and
- 78% sensitivity and 61% specificity (AUC=0.74) on a replication set of 60 independent cases and 2,863 unmatched controls.
We wanted to understand the meaning of these results and to determine whether this model could be used to predict longevity for 23andMe customers. To this end, we examined a few specific aspects of the study in closer detail.
1. Performance on discovery data.
Our first area of interest was in understanding the authors’ proposed methodology for constructing the predictive models. In the paper, the authors describe a procedure for constructing an ensemble of nested predictive models, using SNPs that were identified as the top associations in a GWAS. To choose between different models, the authors described a procedure that involved repeatedly splitting the discovery set into training and testing folds; however, in each case, the set of SNPs that were candidates for inclusion were taken from the top hits in the GWAS of the entire discovery set. We were concerned that constructing models in this way could lead to extremely biased estimates of accuracy since the candidate SNP selection process uses information from the testing folds.
To evaluate this, we simulated genome-wide association studies of 801 cases and 914 controls across 200,000 independent SNPs, one representing the true association with rs2075650, and the other 199,999 not associated with longevity (reduced from the 243,980 SNPs in the paper to account for potential non-independence in the original set). In each simulation, we selected the 281 most strongly associated SNPs and built nested prediction models as described in the longevity study. Across 1,000 simulated datasets, when we evaluated the resulting models by 10-fold cross validation, we observed an average sensitivity of 88%, an average specificity of 89%, and an average AUC of 0.95, very close to the reported values. Thus, the reported performance in the discovery data seems consistent with the null hypothesis that rs2075650 is the only informative SNP in the model, and the performance difference between a 281-SNP model and a 1-SNP model could be entirely explained by overfitting.
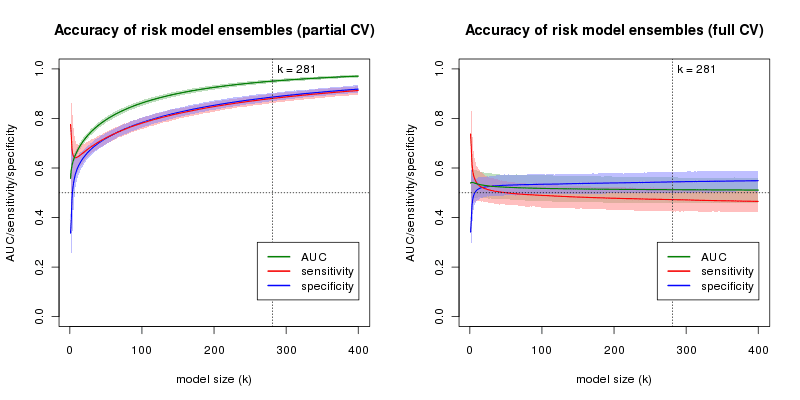Performance of risk model ensembles from Sebastiani et al. 2012, trained on simulated random data containing only one true association. The left plot shows 10-fold cross-validation performance when SNPs are pre-selected using the entire discovery sample. The right plot shows 10-fold cross-validation performance when no SNPs are pre-selected. Shaded regions denote 95% confidence bands. Note the similarity of the sensitivity and specificity curves in the left plot with Figures 4B and S4A from the paper, which the authors use to justify including 281 SNPs in their model. In contrast, in the right plot, model accuracy (in terms of AUC) decreases with increasing model size.Although the authors do acknowledge the possibility of overfitting, we suspect that some readers may be surprised at the extent to which “pre-selecting” candidate SNPs for a model (based on the results of a genome-wide scan where the validation set has not been excluded) can lead to highly inflated estimates of accuracy, even when the underlying data is essentially random. In particular, these results cast doubt on the validity of the resampling experiments used by the authors to justify their choice of model size since the predictive accuracies estimated by the authors’ bootstrapping procedure are just as vulnerable to overfitting the discovery data as the cross-validation protocol in our simulation above.
Had SNP selection been performed in the “inner loop” of the validation (i.e., only using the training portion of each train/test split), then the estimates of performance for different models would not have suffered from the bias shown here and substantial overfitting could have been avoided. In the simulations above, if one uses a correct cross-validation procedure, model accuracy decreases with model size, consistent with the fact that there is just one true association in the data.
2. Population stratification in 23andMe data.
Of course, even a model that is overfit may have some amount of predictive power as long as the “noisy” predictions from the model show some meaningful correlation with true phenotypes. Our second step was to implement the 281-SNP model described in Table S1 of the paper and test it in a collection of over 80,000 23andMe research participants with predominantly European ancestry.
In preparation for assessing the performance of the model, we examined whether there was any evidence that the risks predicted by the model varied with ancestry in the 23andMe data. We used principal components analysis to extract the two most important dimensions of ancestry in these individuals, and plotted the proportion of individuals with predicted probability of exceptional longevity (according to the model) > 0.5 for 23andMe participants on these dimensions. Because living to age 100 is so rare, this plot effectively shows the false positive rate of the classifier, or “1-specificity”, in 23andMe participants, assuming a prior probability of exceptional longevity of 0.5 to be consistent with results in the paper.
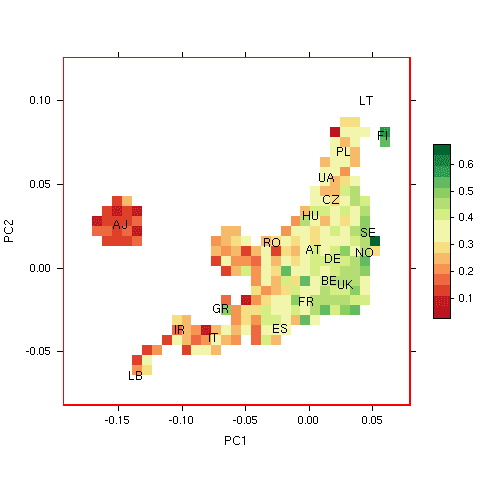Proportion of individuals in 23andMe database with predicted longevity probability > 0.5 based on Sebastiani’s model. (LB=Lebanon, IR=Iran, IT=Italy, GR=Greece, ES=Spain, FR=France, BE=Belgium, UK=United Kingdom, RO=Romania, HU=Hungary, AT=Austria, DE=Denmark, NO=Norway, SE=Sweden, CZ=Czech Republic, UA=Ukraine, PL=Poland, FI=Finland, LT=Lithuania).In the figure to the right, we show results for areas of the plot with at least 50 participants. The labels indicate country of origin for participants with four grandparents from the same country, or ‘AJ’ for self-identified Ashkenazi Jews. We see a trend in risk scores, with lower probabilities of longevity assigned to Ashkenazi Jews, Southern, and Eastern Europeans compared to Western and Northern Europeans. Specificity of the model varies from >70% for Ashkenazi Jews to <50% for Scandinavians.
The plot provides evidence that the overall risk scores predicted by the model correlate with ancestry in the 23andMe population. Although this observation might seem surprising, given that the risk model was trained on cases and controls that were matched for genetic ancestry, there is no contradiction here — it is plausible that the genetic component of exceptional longevity might vary systematically with ancestry. Furthermore, it is certainly true that individual alleles in the risk model are in some cases correlated with ancestry; for instance, rs2075650 near APOE shows a gradient in minor allele frequency from south to north across Europe.
The fact that the risk score from the model stratifies by ancestry suggests that the latter should be taken into account as a potential confounding factor when measuring performance, especially when comparing performance in datasets with differing composition by ancestry. This result might complicate interpretation of the authors’ second replication experiment, because that experiment used cases and controls that were not matched for ancestry. (In the paper, the authors did look for such an effect, but Fig. S10 does not provide strong evidence for the absence of residual population stratification.)
3. Performance on 23andMe data.
From the 23andMe research database we selected a cohort of unrelated individuals of primarily European ancestry, including 31,547 participants with current age < 50, and 2,506 participants with age >= 80. Using logistic regression, we tested whether there was an association between longevity (age >= 80) and the predicted longevity score (converted to log-odds), adjusting for gender. Interestingly, despite the model overfitting described earlier, we found a weak but significant association between the two (P=0.021, odds ratio (OR) = 1.03).
However, we saw a stronger association between longevity and the single APOE SNP rs2075650 (P=2.8e-5, OR=0.83); this association was the only statistically genome-wide significant association in the authors’ analysis as well. We also saw a strong association between longevity and the first five principal components of ancestry (P= 100), the association with rs2075650 was no longer significant but had a larger effect size in the expected direction (P=0.075, OR=0.44). The longevity risk score was still not associated with age (P=0.97) after controlling for ancestry and the APOE SNP, a result which is not particularly sensitive to the age cutoff used (P=0.30 using 479 individuals with age >= 90, or P=0.28 using 141 individuals with age >= 95).
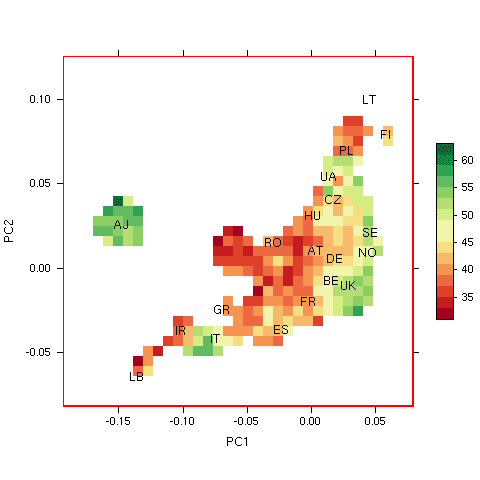Median age of 23andMe research participants by self-identified (AJ) or 4-grandparent-determined ancestry.There are multiple reasons why the risk score might not replicate in the 23andMe cohort. For example, our younger longevity phenotypes are less extreme than the phenotypes in the PLoS ONE study, and our small group of centenarians has lower power for detecting small effects on risk. In addition, our self-reported age data may be less reliable for extreme ages, though to reduce the risk of errors from incorrect age reporting, the above analyses were conservatively restricted to individuals who provided their date-of-birth in at least two separate forms or surveys on the 23andMe website and excluded those who reported conflicting birth years in any of these locations.
Interestingly, in our cohort, Ashkenazi Jewish ancestry is positively associated with longevity (for age >= 80: P=3.4e-4, OR=2.2), while in the PLoS ONE study, Ashkenazi Jewish ancestry seems to be negatively associated with longevity. This almost certainly reflects a difference in how individuals were selected for the two studies, rather than a difference in genetic predispositions. If we exclude Ashkenazi Jews from our regression analysis, the longevity score is slightly more predictive on its own (P=0.019, OR=1.03), but the association again goes away once we add the top five principal components and APOE to the model (P=0.22, OR=1.02).
Concluding thoughts
The genetic model presented by Sebastiani and Perls appears to be overfit to their training data, and we further see very little correlation between the predictive scores generated from their model and longevity in the 23andMe research cohort, once the effects of ancestry and the significant APOE association are taken into account. Even without these additional corrections, the ability of the authors’ risk score to distinguish long-lived individuals in our database is poor.
It is worth noting that a model based on only the single APOE association in the paper achieves an AUC of 0.58 (0.52-0.63) among individuals with age >= 100 in the 23andMe cohort, consistent with the authors’ estimate of 0.62; the effect weakens with decreasing age cutoff (e.g., AUC=0.53 (0.49-0.56) for age >= 95). When combined with the 280 other SNPs in the authors’ model, however, the performance in our cohort drops to AUC=0.49 (0.39-0.60) among centenarians (or AUC=0.52 (0.47-0.56) for age >= 95), which is statistically indistinguishable from random guessing. While the ability of our cohort to detect meaningful association may be limited due to sample size, our confidence intervals are at least sufficiently narrow to exclude the point estimate of AUC=0.74 reported by the authors for their second replication study.
We remain concerned that despite clear improvements in the authors’ revised study, the analysis may nonetheless be susceptible to subtle biases, due to the way in which cases and controls were selected. Because of the numerous potential confounding factors related to the separate ascertainment of cases and controls and the fact that most of the controls were derived from a single source, it may be impossible to formally show that all sources of bias have been adequately controlled in the authors’ analyses.
An alternative analysis that at least partially addresses some of the concerns above (without genotyping additional samples) would be to repeat the discovery analysis using a random subset of NECS cases and Illumina controls (using a properly cross-validated model selection procedure), and reserving the remainder of the NECS cases and controls for replication. This would not resolve the potential for confounding in the model building step, but would at least reduce the potential for bias in the replication set. A more convincing demonstration would require constructing and evaluating the model using a dataset where such confounding factors are simply absent by design (i.e., where cases and controls are drawn from a single underlying population and genotyped together); this would certainly involve genotyping of more controls than in the study, but unlike centenarians, controls are relatively easy to come by (we have lots!).
In our view a predictive genetic model for longevity remains elusive but we are optimistic that continuing efforts like the New England Centenarian and Supercentenarian Studies will keep adding to our knowledge of this most human of traits.
